선도예금

Weneedu 2020. 4. 12. 09:43

선도금리계약을 이해하기 위해 우리가 익숙한 예금상품을 먼저 생각해보자.

지금 은행 창구에 가서 돈 100만원을 내면 1년짜리 정기예금을 들 수 있다, 요즘은 창구에 가지 않아도 인터넷이나 스마트폰으로 가입할 수도 있을 테지만 어쨌거나 지금 돈을 은행에 주면 가입할 수 있는 예금, 이 예금은 정확히 말하자면 현물 예금이다. 그런데 지금은 돈이 없지만 1년 뒤에 돈이 100만원 생길 예정이고 그때 1년만기 예금을 들고싶다, 그런데 그 금리를 지금 확정하고 싶다면, 어떻게 해야할까? 이때 필요한 것이 선도 예금이다.

현물예금에 상대되는 개념으로도 선도예금을 생각할 수 있다. 현물예금이 지금 예금에 가입하고, 미래의 만기시점에 되돌려 받는 거래라면, 선도예금은 지금 계약을 체결하고, 미래에 예금에 가입한 뒤 그 뒤 시점에 원금과 이자를 돌려받는 거래를 말한다.

은행에서 이런 상품을 팔지는 않지만 선도예금이 있다면 1년 뒤 가입할 1년만기 정기예금의 금리를 지금 확정할 수 있는 것이다, 선도 예금은 현물 예금을 이용해서 복제할 수도 있다, 1년 만기 정기예금과 2년 만기 정기예금리 있다면 1년 뒤 가입할 1년 만기 정기예금 즉 선도예금을 만들 수 있다,

방법은 이렇다, 우선 100만원 어치 2년짜리 정기예금에 가입한다, 그런데 지금 돈이 없으니 100만원을 빌려야 한다. 그래서 1년 만기 정기예금을 발행한다, 그러면 지금 돈은 하나도 들어가지 않은 상태가 된다, 1년 뒤 만기가 된 정기예금을 돌려줘야 한다. 그런데 나에게는 100만원이 들어오기로 되어있었다, 그 돈으로 만기가 된 정기예금을 돌려주면 된다, 즉 1년 차에 내 돈 100만원이 나간다, 그리고 2년 차에 2년전에 가입했던 2년 만기 정기예금이 만기가 되고 원금과 이자를 받게 된다, 이 거래에서 각 시점(현재, 1년차 2년차)에 발생하는 현금흐름을 따져 보면 우리가 원했던 선도예금의 현금흐름과 동일한 것을 알 수 있다,

구체적으로 숫자예를 살펴보자.

“앞으로 1년 뒤에 100만원을 1년 간 예금하려고 하는 고객이 있을 때 예금금리로 얼마를 제시해야 할까?”

미래(1년 뒤)의 예금금리라 현재 시점에는 알 수 없다고 할 수도 있겠지만, 1년과 2년 정기예금 금리가 정해져 있다면, 현재 이 예금의 금리를 확정할 수 있는 방법이 있다. 다음 2년간100만원을 투자하는 두 전략을 생각해보자.

전략1: 1년 동안 100만원을 예금한 뒤 다시 1년을 예금

전략2: 2년 동안 100만원을 예금

1년 정기예금금리를 3%, 2년 정기예금금리를 4%, 고객이 요구한 예금금리를 R라고 하자.

위 두 전략은 2년 시점에 동일한 결과(원금과 이자)를 제공해야 한다(만약 그렇지 않다면 차익거래(Arbitrage)가 발생한다). 따라서 다음이 성립한다.

전략1의 만기수익=전략2의 만기수익 ⟶ 100*(1+3%)*(1+R)=100*(1+2*4%)

즉 R=(1+2*0.04)/(1+0.03)-1=0.0485(4.85%)이어야 한다.

선도예금의 손익은 어떻게 정해질까?

예를 들어 지금 계약을 체결하는데, 3개월 뒤에 예금을 가입하고 그 3개월 뒤에 만기가 되는 선도예금 계약을 생각해보자. 계약시점에는 예금금액(계약금액;N)과 예금금리(계약금리;K)가 정해져야 할 것이다. 이 계약의 손익은 3개월 뒤 시점에 현물 이자율에 따라서 정해질 것인데, 그림으로 표시하면 다음과 같다.

예를 들어 100만원을 3개월 뒤 3개월 정기예금에 3%이율로 가입하기로 계약한 경우를 생각해보자. 3개월 뒤 3개월 정기예금금리가 4%가 되었다면, 선도예금계약으로 인해 시중 예금금리보다 낮은 3%에 예금을 가입하는 결과가 되므로 1000000*1%*3/12=2500(원)을 손해 보는 셈이고, 반대로 시중예금금리가 2%로 되었다면 2500(원) 이익을 얻게 된다.

따라서 선도예금계약의 자금회수시점 손익은 다음과 같이 정해진다.

N=예금원금

K=계약금리

t_1=자금투입시점

t_2=자금회수시점

A=(t_1,t_2)기간 날짜수

위 결과를 일반적인 경우로 확장해보면 다음과 같다.

우선 표기의 편의를 위해 t1 시점에 계약을 체결하고, t2시점에 자금을 투입하며, t3시점에 자금을 회수하는 거래의 이자율을 다음과 같이 표시하자(t1,t2,t3는 연율이다. 예를 들어 t1이 3개월이라면 t1=0.25가 된다).

예를 들어 현재 계약을 체결하고 3개월 뒤에 자금을 투입하며, 그 3개월 뒤에 자금을 회수하는 투자의 이자율은 다음과 같이 표기할 수 있다.

R(0,0.25,0.5)

현물이자율은 계약시점과 자금투입시점이 일치하므로 위 표기법에 따르면 R(t1,t1,t2)으로 표현할 수 있는데, 편의 상 중복되는 두 개항을 합쳐서 다음과 같이 쓸 수도 있다.

R(t1,t1,t2)=R(t1,t2)

즉 기간표시 항목이 2개인 경우는 현물이자율에 대한 표기이며, 기간표시 항목이 3개인 것은 선도이자율에 대한 표기이다.

이제 미래의 t1시점과 t2시점간에 투자하는 경우 수익률은 다음과 같이 정해진다.

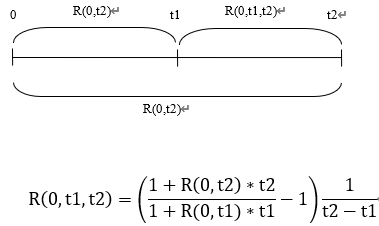
이렇게 정해진 선도금리를 내재선도금리(Implied Forward Rate)라고 한다.

이 식은 현물 금리와 선도 금리 사이의 관계를 나타내는 것으로 볼 수도 있다.