20230426 1254
결론
단순 perceptron은 logistic regression과 동일하다. ★★★★★
see wiki logistic regression
질문
OR, AND gate를 fitting할 때, 왜 최소자승법 or linear regression을 적용하면 안될까?
->된다
0. 말로 설명하기
① 회귀식을 정하고 : y = w1x1+w2x2+b .........(식1)

② 데이터를 정하고 : x1,x2, y는 다음과 같다(OR Gate의 경우)
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
③ 최소자승법 적용하고: (x'x)^(-1)x'y = beta^

④ 결과는 (w1, w2, b) = (0.5, 0.5, 0.25)나온다.
⑤ 결과를 회귀식에 적용해보면
| x1 | x2 | y^ |
| 0 | 0 | 0.25 |
| 0 | 1 | 0.75 |
| 1 | 0 | 0.75 |
| 1 | 1 | 1.25 |
⑥ (해석) 0.5를 경계로 보면(0.5 이상을 1, 0.5 이하를 0으로 보면) 위 결과는 (0, 1, 1, 1)과 같고 따라서 정답이다.
0.5를 경계로 보아야하는 이유
종속변수가 0 또는 1이므로 이를 피팅한 결과는 0 또는 1에 가까운 어떤 수일 것이다. 그 둘을 나누는 지점을 하나 잡아야 한다면 그 지점은 0.5가 되어야 할 것이다. 따라서 회귀식은 0.5를 기준으로 0과 1을 구분하는 결과를 보여 줄 것이다.
즉 (x1, x2) 평면상에 경계선 그래프를 그릴 때 다음 식을 사용해야 한다.
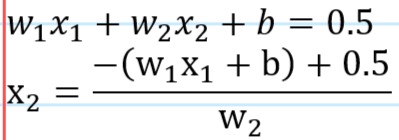
등고선 개념.
1. Excel로 해보자
20230425 1813 deep learning.xlsx
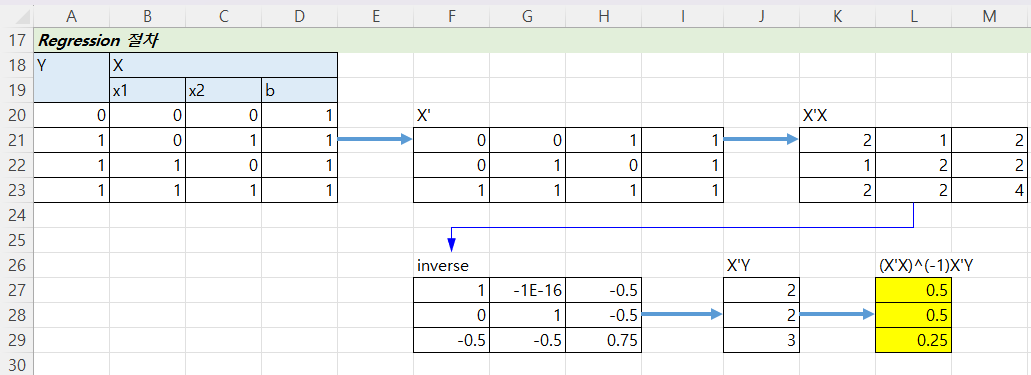


(note) 위 두 그림의 관계는 다음과 같다(★빨간 색에 노란 형광색 칠해진 선은 모두 동일하다).

2 Python으로 해보자
# OXR gate 데이터로 회귀식에 피팅해보자.
# (x'x)^(-1)x'y = beta
import numpy as np
import matplotlib.pyplot as pl
b = 1
x=np.array([[0,0,b],[0,1,b],[1,0,b],[1,1,b]])
y=np.array([0,1,1,1]) #OR
#y=np.array([0,0,0,1]) #AND
# y=np.array([0,1,1,0]) #XOR
print(x)
xt = np.matrix.transpose(x)
print("transpose:",xt)
a = np.matmul(xt,x)
print("multi:",a)
bb = np.linalg.inv(a)
print("inv:",bb)
c = np.matmul(bb,xt)
d = np.matmul(c,y)
print("sol:",d)
def f(x):
ans = d[0]*x[0]+d[1]*x[1]+d[2]*x[2]
return ans
y = f([0,0,1])
print("ff: ", y)
y = f([0,1,1])
print("ft: ", y)
y = f([1,0,1])
print("tf: ", y)
y = f([1,1,1])
print("tt: ", y)
x1 = np.array([0,1])
x2 = (-d[2]-d[0]*x1+0.5)/d[1]
pl.plot(x1,x2)
pl.plot(0,0,'x')
pl.plot(1,0,'o')
pl.plot(0,1,'o')
pl.plot(1,1,'o')실행결과

'[AI]Artificial Inteligence 인공지능' 카테고리의 다른 글
| AI 로지스틱 회귀 Logistic Regression (0) | 2023.04.30 |
|---|---|
| AI 활성화 함수 Activation Function (0) | 2023.04.30 |
| AI deep learning도 error minimizing 개념 (0) | 2023.04.24 |
| AI 큰 그림 Story telling of Deep Learning (1) | 2023.04.15 |
| AI Newton Raphson method 이해 (0) | 2023.04.11 |




