20220205 2157
REF
허수에 대해 먼저 보고
[1] "https://www.youtube.com/watch?v=Bg08-ayRubU", 3편
[2] "https://www.youtube.com/watch?v=dUcf7oIRpNA&t=3s" 2편
[3] "https://www.youtube.com/watch?v=udLD8jQ6X-k" 1편
[4] "https://m.blog.naver.com/galaxyenergy/221232517720" 복소수 지수의 이해..쓸데없는 그림이 많음
★★★
모든 수는 (수직선 상의 한) 점이다.
모든 연산은 그 점을 다른 곳으로 옮기는 행위이다.
★★★
(예) 3에 -1을 곱하는 것은 (0을 중심으로) 반대로 옮겨놓는 건데.. 이게 1차원(직선)이라 왼쪽 아니면 오른쪽 밖에 없어서 잘 안보이지만, "방향을 바꿔주는 것"이다
복소평면에서 보면 -1을 곱하는 것이 방향을 바꾸는 것이란게 명확히 보인다.
수의 확장
자연수 → 0(whole number) → 음수(정수) → 유리수 → 무리수(실수) → 허수
복소평면에서
(-1)을 곱하는 것의 의미 ; 1 * (-1)
⬇️
i를 곱하는 것의 의미 ; 1 * i
⬇️
e^ix의 의미 [1]
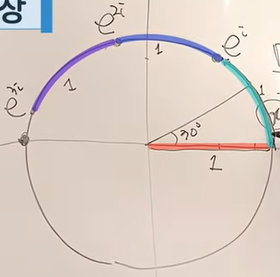
e^i => 반지름 1인 원에서 호 Arc의 길이가 1인 지점1
(note) e^i는 위치가 왜 저기일까?...이 질문에 답하기 전에 e에 i번 제곱하다는 것의 의미를 먼저 알아야 한다.
★★★★ 지수의 확장
지수가 자연수인 경우는 직관적으로 이해가 되는데...
지수가 0?
지수가 음수?
지수가 유리수?
지수가 무리수?
지수가 허수?
→ 지수를 실수까지 확장하는건 그래도 어느 정도 이해되는데...문제는 허수의 지수; 새로운 차원의 생각이 필요
거듭제곱이 실수가 아닐 경우, "자기자신을 몇번 곱한 수"라는 식의 정의로 이해 할 수 없다!2
→ 새로운 정의가 필요하다!!!!!!!!!!!!!!!!!!!
① "오일러상수, 자연상수, 자연로그의 밑"의 정의에서
e = lim_n->inf (1+1/n)^n = 1 + 1/2! + 1/3! + ...
e = 극한 정의 = 무한급수 정의
② 오일러 상수의 지수의 해석적 정의(맞나?)
lim_n->inf(1+m/n)^n = lim_n->inf(1+m/n)^n/m*m) = @
let n/m = z, @ = lim_z->inf [(1+1/z)^z]^m = [lim_z->inf(1+1/z)^z]^m (단, lim와 지수연산이 교환 가능하다고 가정) = e^m
즉, e^m = lim_n->inf(1+m/n)^n으로 정의할 수 있다.
(놀라운 점) e^i는 e의 거듭제곱이 아니라 유리수 다항식의 극한이다.
즉 대략 e^x ~ (1+x/2)^2라고 생각하자!3
결론
| 오일러 항등식은 복소평면상의 (-1,0)인 점을 다르게 표현한 것일 뿐이다! * 복소평면은 복소수의 실수부를 x, 허수부를 y로 나타내는 공간이다. |
'퀴즈' 카테고리의 다른 글
| 삼각함수 미분의 직관적 이해 (0) | 2022.02.24 |
|---|---|
| 아들 딸 문제 (0) | 2022.02.21 |
| 몬티홀 문제 (0) | 2022.02.04 |
| 로그함수의 적분 (0) | 2022.02.04 |
| 수학이 실생활에 필요한 사례 - 보안 (0) | 2022.01.23 |




